
En este caso, la fuerza que actúa sobre el cuerpo perpendicularmente al plano de deslizamiento es su peso Peso = m · g y según la figura de la derecha, es obvio que N=Peso=m·g (1) (como vemos en la cruz de fuerzas del sistema). Por tanto, la fuerza de rozamiento valdrá: Fr=µ·N=µ·m·g. La fuerza efectiva que dé origen a la aceleración del objeto será: Fefectiva=Faplicada-Fr=Fa-µ·m·g (2).
Para resolver problemas de este tipo tendremos en cuenta el Segundo Principio de Newton (F=m·a) e igualaremos esta fuerza al producto de la aceleración por la masa del objeto. Así pues, reajustaremos la ecuación para despejar la incógnita que nos pidan. Normalmente ésta será la aceleración del sistema. Por lo tanto: m·a = Fa-µ·m·g, de donde: a=(Fa-µ·m·g)/m.
Si el objeto no es empujado, sino que se abandona libremente a sí mismo, no habrá fuerza aplicada. La aceleración vendrá dada por: a=-(µ·m·g)/m.
Caída de un cuerpo por un plano inclinado:
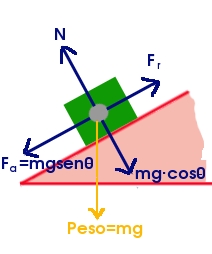
Si se trata de un plano inclinado la cruz de fuerzas del sistema queda como vemos a la derecha. Esta vez, la fuerza que produce el movimiento de caída no es únicamente el peso del cuerpo sino su componente en la dirección del plano, el seno del ángulo de inclinación. Y la fuerza normal N es la componente del peso que va en dirección perpendicular al plano, el coseno del ángulo de inclinación. Es decir, que la fuerza aplicada a la caída será: Fa=m·g·senα, y la normal: N=m·g·cosα.
El valor de la fuerza de rozamiento será: Fr=µ·N=µ·m·g·cosα.
Por lo tanto, la fuerza efectiva será la suma de fuerzas del sistema: F=Fa-Fr=m·g·senα-µ·m·g·cosα.
Si aplicamos la Segunda Ley de Newton, la ecuación fundamental de la dinámica de traslación (F=m·a), podemos plantear:
m·a=m·g·senα-µ·m·g·cosα de donde: a=g·senα-µ·g·cosα=g(senα-µ·cosα).
No hay comentarios:
Publicar un comentario